Radix sort

Introduction to Radix Sort

Radix sort is a non-comparative integer sorting algorithm. It sorts integers by processing individual digits. Starting from the least significant digit (LSD) to the most significant digit (MSD), it uses a stable subroutine sort (like counting sort) to handle the individual digits. The algorithm is efficient for sorting numbers with a fixed number of digits and works well when the range of digits is not excessively large.

Steps of Radix Sort (Pseudocode Steps)

1. Find the maximum number to determine the number of digits.
2. Initialize: Set up a loop to process each digit from the least significant to the most significant.
3. Digit by digit sorting:
   • Use a stable sort (e.g., counting sort) to sort based on the current digit.
4. Repeat until all digits are processed.

Example

To perform radix sort on the array [170, 45, 75, 90, 802, 24, 2, 66], we follow these steps:

Step 1: Find the largest element in the array, which is 802. It has three digits, so we will iterate three times, once for each significant place.

Step 2: Sort the elements based on the unit place digits (X=0). We use a stable sorting technique, such as counting sort, to sort the digits at each significant place.

Sorting based on the unit place:

Perform counting sort on the array based on the unit place digits. The sorted array based on the unit place is [170, 90, 802, 2, 24, 45, 75, 66].

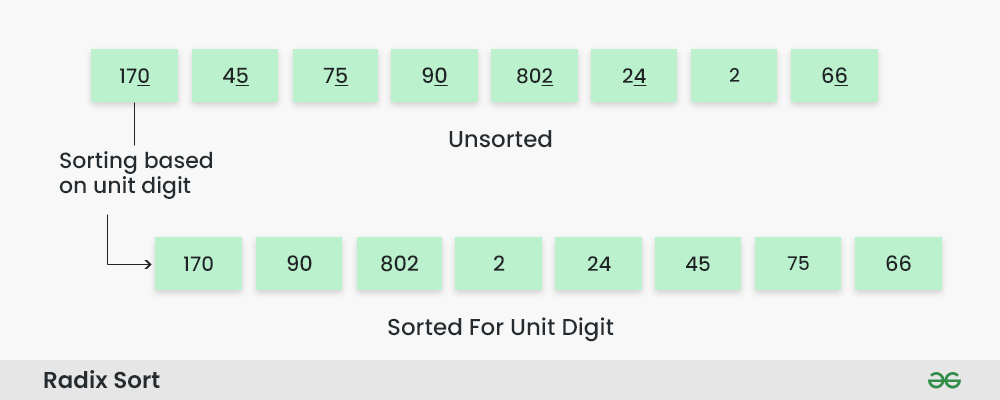
Step 3: Sort the elements based on the tens place digits.

Sorting based on the tens place:

Perform counting sort on the array based on the tens place digits. The sorted array based on the tens place is [802, 2, 24, 45, 66, 170, 75, 90].

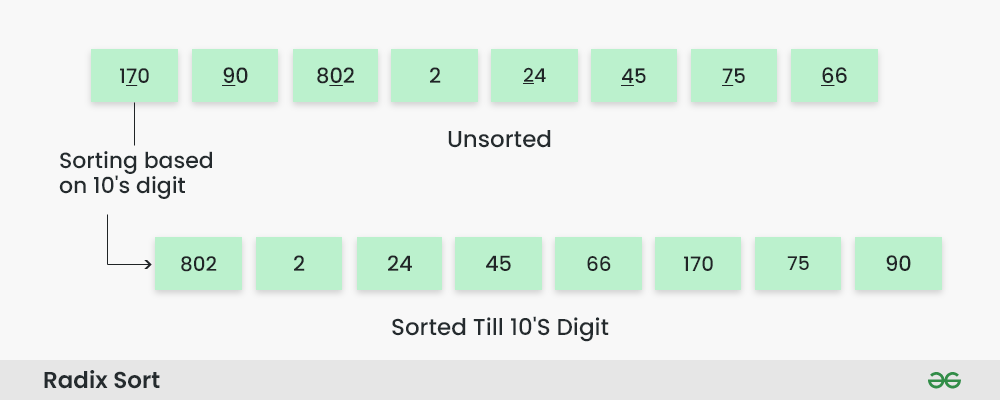
Step 4: Sort the elements based on the hundreds place digits.

Sorting based on the hundreds place:

Perform counting sort on the array based on the hundreds place digits. The sorted array based on the hundreds place is [2, 24, 45, 66, 75, 90, 170, 802].

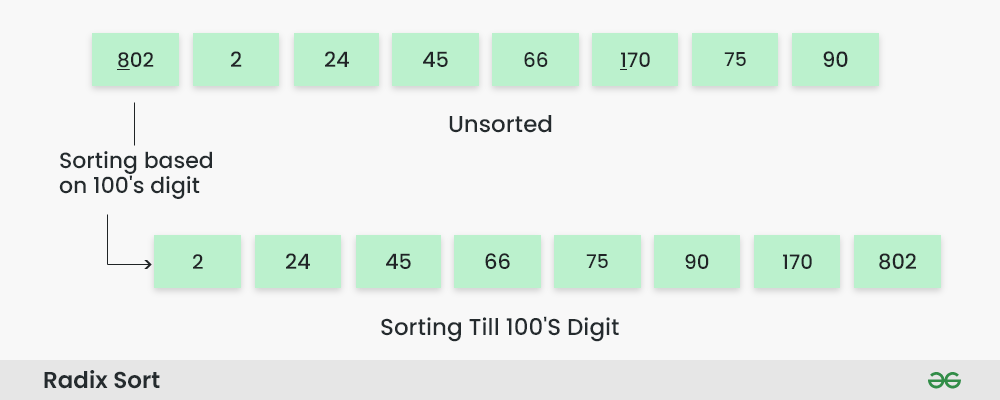
Step 5: The array is now sorted in ascending order.

The final sorted array using radix sort is [2, 24, 45, 66, 75, 90, 170, 802].

Pseudocode for Radix Sort

function radixSort(array):
    maxNumber = findMax(array)
    numberOfDigits = countDigits(maxNumber)

    for digit in 1 to numberOfDigits:
        countingSortByDigit(array, digit)

function findMax(array):
    maxNumber = array[0]
    for number in array:
        if number > maxNumber:
            maxNumber = number
    return maxNumber

function countDigits(number):
    count = 0
    while number != 0:
        number = number // 10
        count += 1
    return count

function countingSortByDigit(array, digit):
    count = array of size 10 initialized to 0
    output = array of same size as input array

    # Count occurrences of each digit
    for number in array:
        digitValue = (number // 10^(digit - 1)) % 10
        count[digitValue] += 1

    # Change count[i] so that count[i] contains the position of this digit in output
    for i from 1 to 9:
        count[i] += count[i - 1]

    # Build the output array
    for i from length(array) - 1 to 0:
        digitValue = (array[i] // 10^(digit - 1)) % 10
        output[count[digitValue] - 1] = array[i]
        count[digitValue] -= 1

    # Copy the output array to the input array
    for i from 0 to length(array) - 1:
        array[i] = output[i]

Radix Sort Implementation in Python, C++, Java and JavaScript

Python

def radix_sort(array):
    def counting_sort_by_digit(array, digit):
        count = [0] * 10
        output = [0] * len(array)

        for number in array:
            digit_value = (number // 10**(digit - 1)) % 10
            count[digit_value] += 1

        for i in range(1, 10):
            count[i] += count[i - 1]

        for i in range(len(array) - 1, -1, -1):
            digit_value = (array[i] // 10**(digit - 1)) % 10
            output[count[digit_value] - 1] = array[i]
            count[digit_value] -= 1

        for i in range(len(array)):
            array[i] = output[i]

    max_number = max(array)
    number_of_digits = len(str(max_number))

    for digit in range(1, number_of_digits + 1):
        counting_sort_by_digit(array, digit)

# Example usage
arr = [170, 45, 75, 90, 802, 24, 2, 66]
radix_sort(arr)
print(arr)

C++

#include <iostream>
#include <vector>
#include <algorithm>

void countingSortByDigit(std::vector<int>& array, int digit) {
    int size = array.size();
    std::vector<int> output(size);
    int count[10] = {0};

    for (int i = 0; i < size; i++) {
        int digitValue = (array[i] / digit) % 10;
        count[digitValue]++;
    }

    for (int i = 1; i < 10; i++) {
        count[i] += count[i - 1];
    }

    for (int i = size - 1; i >= 0; i--) {
        int digitValue = (array[i] / digit) % 10;
        output[count[digitValue] - 1] = array[i];
        count[digitValue]--;
    }

    for (int i = 0; i < size; i++) {
        array[i] = output[i];
    }
}

void radixSort(std::vector<int>& array) {
    int maxNumber = *max_element(array.begin(), array.end());
    for (int digit = 1; maxNumber / digit > 0; digit *= 10) {
        countingSortByDigit(array, digit);
    }
}

// Example usage
int main() {
    std::vector<int> arr = {170, 45, 75, 90, 802, 24, 2, 66};
    radixSort(arr);
    for (int num : arr) {
        std::cout << num << " ";
    }
    return 0;
}

Java

import java.util.Arrays;

public class RadixSort {

    public static void radixSort(int[] array) {
        int maxNumber = Arrays.stream(array).max().getAsInt();
        for (int digit = 1; maxNumber / digit > 0; digit *= 10) {
            countingSortByDigit(array, digit);
        }
    }

    private static void countingSortByDigit(int[] array, int digit) {
        int size = array.length;
        int[] output = new int[size];
        int[] count = new int[10];

        for (int i = 0; i < size; i++) {
            int digitValue = (array[i] / digit) % 10;
            count[digitValue]++;
        }

        for (int i = 1; i < 10; i++) {
            count[i] += count[i - 1];
        }

        for (int i = size - 1; i >= 0; i--) {
            int digitValue = (array[i] / digit) % 10;
            output[count[digitValue] - 1] = array[i];
            count[digitValue]--;
        }

        for (int i = 0; i < size; i++) {
            array[i] = output[i];
        }
    }

    public static void main(String[] args) {
        int[] arr = {170, 45, 75, 90, 802, 24, 2, 66};
        radixSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

JavaScript Code Implementation

function countingSortByDigit(array, digit) {
    const size = array.length;
    const output = new Array(size);
    const count = new Array(10).fill(0);

    // Count occurrences of each digit
    for (let i = 0; i < size; i++) {
        const digitValue = Math.floor((array[i] / digit) % 10);
        count[digitValue]++;
    }

    // Update count array to get the actual position of digits
    for (let i = 1; i < 10; i++) {
        count[i] += count[i - 1];
    }

    // Build the output array
    for (let i = size - 1; i >= 0; i--) {
        const digitValue = Math.floor((array[i] / digit) % 10);
        output[count[digitValue] - 1] = array[i];
        count[digitValue]--;
    }

    // Copy the output array to the original array
    for (let i = 0; i < size; i++) {
        array[i] = output[i];
    }
}

function radixSort(array) {
    const maxNumber = Math.max(...array);
    for (let digit = 1; Math.floor(maxNumber / digit) > 0; digit *= 10) {
        countingSortByDigit(array, digit);
    }
}

// Example usage
const arr = [170, 45, 75, 90, 802, 24, 2, 66];
radixSort(arr);
console.log(arr.join(" ")); // Output: 2 24 45 66 75 90 170 802

Explanation of the Code

1. Function countingSortByDigit:

   • This function sorts the array based on the specified digit.
   • It initializes an output array and a count array to store occurrences of digits.

2. Counting Occurrences:

   • For each element, it extracts the digit value and increments the corresponding count.

3. Building the Output Array:

   • It calculates the actual positions of each digit by accumulating the counts.
   • Then it builds the output array by placing each element in its correct position based on the current digit.

4. Copying the Output:

   • Finally, it copies the sorted output back to the original array.

5. Function radixSort:

   • This function finds the maximum number in the array to determine the number of digits.
   • It repeatedly calls countingSortByDigit, incrementing the digit value by a factor of 10 each time.

6. Example Usage:

   • An example array arr is sorted using radixSort, and the sorted array is printed to the console.

Complexity of Radix Sort

• Time Complexity: $O(d⋅(n+k))$
  • $d$ : Number of digits in the largest number.
  • $n$ : Number of elements in the array.
  • $k$ : Range of the digits for decimal system, $k = 10.$
• Space Complexity: $O(n + k)$
  • $n$ : Number of elements in the array.
  • $k$ : Range of the digits for decimal system, $k = 10.$

Conclusion

Radix sort is a powerful sorting algorithm for integers or fixed-length strings. Its efficiency and non-comparative nature make it a valuable tool for specific use cases, especially where the number of digits or characters is limited. Understanding and implementing radix sort can significantly enhance the performance of sorting operations in such scenarios.