Blocked Queue Data Structure

Introduction to Blocked Queue

A blocked queue is a linear data structure that follows the First In First Out (FIFO) principle, similar to a regular queue. However, it includes mechanisms to block and unblock threads when the queue is empty or full. This is particularly useful in concurrent programming where multiple threads may need to access the queue simultaneously.

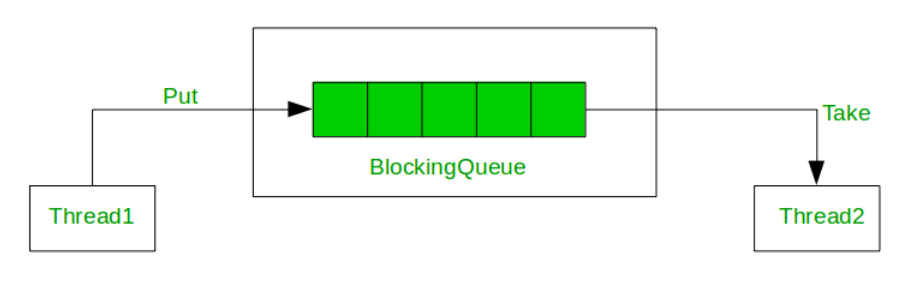
alt text

Blocked Queue Operations

Enqueue: Add an element to the back of the queue.
Dequeue: Remove the element from the front of the queue.
Peek: Retrieve the element at the front of the queue without removing it.
isEmpty: Check if the queue is empty.
isFull: Check if the queue is full.
Size: Get the number of elements in the queue.

Pseudocode

Basic Operations

Enqueue:

function enqueue(blockedQueue, element):
     if isFull(blockedQueue):
          blockThread()  // Block the thread until space is available
     blockedQueue.rear = (blockedQueue.rear + 1) % blockedQueue.size
     blockedQueue.elements[blockedQueue.rear] = element
     unblockThread()  // Unblock any waiting threads

Dequeue:

function dequeue(blockedQueue):
     if isEmpty(blockedQueue):
          blockThread()  // Block the thread until an element is available
     frontElement = blockedQueue.elements[blockedQueue.front]
     blockedQueue.front = (blockedQueue.front + 1) % blockedQueue.size
     unblockThread()  // Unblock any waiting threads
     return frontElement

Peek:

function peek(blockedQueue):
     if isEmpty(blockedQueue):
          return "Queue is empty"
     return blockedQueue.elements[blockedQueue.front]

isEmpty:

function isEmpty(blockedQueue):
     return blockedQueue.front == blockedQueue.rear

isFull:

function isFull(blockedQueue):
     return (blockedQueue.rear + 1) % blockedQueue.size == blockedQueue.front

Size:

function size(blockedQueue):
     return (blockedQueue.rear - blockedQueue.front + blockedQueue.size) % blockedQueue.size

Implementation in Python, C++, and Java

Python Implementation

import threading

class BlockedQueue:
     def __init__(self, size):
          self.size = size
          self.elements = [None] * size
          self.front = 0
          self.rear = 0
          self.lock = threading.Lock()
          self.not_empty = threading.Condition(self.lock)
          self.not_full = threading.Condition(self.lock)

     def enqueue(self, element):
          with self.not_full:
               while self.is_full():
                    self.not_full.wait()
               self.rear = (self.rear + 1) % self.size
               self.elements[self.rear] = element
               self.not_empty.notify()

     def dequeue(self):
          with self.not_empty:
               while self.is_empty():
                    self.not_empty.wait()
               frontElement = self.elements[self.front]
               self.front = (self.front + 1) % self.size
               self.not_full.notify()
               return frontElement

     def peek(self):
          with self.lock:
               if self.is_empty():
                    return "Queue is empty"
               return self.elements[self.front]

     def is_empty(self):
          return self.front == self.rear

     def is_full(self):
          return (self.rear + 1) % self.size == self.front

     def size(self):
          return (self.rear - self.front + self.size) % self.size

# Example usage
bq = BlockedQueue(5)
bq.enqueue(10)
bq.enqueue(20)
print(bq.dequeue())  # Output: 10
print(bq.peek())     # Output: 20
print(bq.is_empty()) # Output: False
print(bq.size())     # Output: 1

C++ Implementation

#include <iostream>
#include <mutex>
#include <condition_variable>
using namespace std;

class BlockedQueue {
private:
     int *elements;
     int front, rear, size;
     mutex mtx;
     condition_variable not_empty, not_full;

public:
     BlockedQueue(int size) {
          this->size = size;
          elements = new int[size];
          front = rear = 0;
     }

     void enqueue(int element) {
          unique_lock<mutex> lock(mtx);
          not_full.wait(lock, [this] { return !is_full(); });
          rear = (rear + 1) % size;
          elements[rear] = element;
          not_empty.notify_one();
     }

     int dequeue() {
          unique_lock<mutex> lock(mtx);
          not_empty.wait(lock, [this] { return !is_empty(); });
          int frontElement = elements[front];
          front = (front + 1) % size;
          not_full.notify_one();
          return frontElement;
     }

     int peek() {
          lock_guard<mutex> lock(mtx);
          if (is_empty()) {
               cout << "Queue is empty" << endl;
               return -1; // Indicating empty
          }
          return elements[front];
     }

     bool is_empty() {
          return front == rear;
     }

     bool is_full() {
          return (rear + 1) % size == front;
     }

     int size_of_queue() {
          return (rear - front + size) % size;
     }

     ~BlockedQueue() {
          delete[] elements;
     }
};

// Example usage
int main() {
     BlockedQueue bq(5);
     bq.enqueue(10);
     bq.enqueue(20);
     cout << bq.dequeue() << endl;  // Output: 10
     cout << bq.peek() << endl;      // Output: 20
     cout << boolalpha << bq.is_empty() << endl; // Output: false
     cout << bq.size_of_queue() << endl; // Output: 1
     return 0;
}

Java Implementation

import java.util.concurrent.locks.Condition;
import java.util.concurrent.locks.Lock;
import java.util.concurrent.locks.ReentrantLock;

public class BlockedQueue {
     private int[] elements;
     private int front, rear, size;
     private final Lock lock = new ReentrantLock();
     private final Condition notEmpty = lock.newCondition();
     private final Condition notFull = lock.newCondition();

     public BlockedQueue(int size) {
          this.size = size;
          elements = new int[size];
          front = rear = 0;
     }

     public void enqueue(int element) {
          lock.lock();
          try {
               while (is_full()) {
                    notFull.await();
               }
               rear = (rear + 1) % size;
               elements[rear] = element;
               notEmpty.signal();
          } catch (InterruptedException e) {
               Thread.currentThread().interrupt();
          } finally {
               lock.unlock();
          }
     }

     public int dequeue() {
          lock.lock();
          try {
               while (is_empty()) {
                    notEmpty.await();
               }
               int frontElement = elements[front];
               front = (front + 1) % size;
               notFull.signal();
               return frontElement;
          } catch (InterruptedException e) {
               Thread.currentThread().interrupt();
               return -1; // Indicating underflow
          } finally {
               lock.unlock();
          }
     }

     public int peek() {
          lock.lock();
          try {
               if (is_empty()) {
                    System.out.println("Queue is empty");
                    return -1; // Indicating empty
               }
               return elements[front];
          } finally {
               lock.unlock();
          }
     }

     public boolean is_empty() {
          return front == rear;
     }

     public boolean is_full() {
          return (rear + 1) % size == front;
     }

     public int size_of_queue() {
          return (rear - front + size) % size;
     }

     public static void main(String[] args) {
          BlockedQueue bq = new BlockedQueue(5);
          bq.enqueue(10);
          bq.enqueue(20);
          System.out.println(bq.dequeue());  // Output: 10
          System.out.println(bq.peek());      // Output: 20
          System.out.println(bq.is_empty());  // Output: false
          System.out.println(bq.size_of_queue()); // Output: 1
     }
}

Complexity

-Time Complexity:

Enqueue: $O(1)$
Dequeue: $O(1)$
Peek: $O(1)$
isEmpty: $O(1)$
isFull: $O(1)$
Size: $O(1)$ -Space Complexity: $O(n)$ , where $n$ is the number of elements that can be stored in the blocked queue.

Example

Consider a blocked queue with the following operations:

Enqueue 10
Enqueue 20
Dequeue
Peek
Check if empty
Get size

Operations:

Enqueue 10: Queue becomes [10, _, _, _, _]
Enqueue 20: Queue becomes [10, 20, _, _, _]
Dequeue: Removes 10, Queue becomes [_, 20, _, _, _]
Peek: Returns 20, Queue remains [_, 20, _, _, _]
isEmpty: Returns false
Size: Returns 1

Conclusion

A blocked queue is an efficient data structure that improves the utilization of space and provides thread safety in concurrent programming scenarios. It is widely used in applications such as producer-consumer problems, task scheduling, and resource management. Understanding and implementing a blocked queue can significantly enhance performance and synchronization in multi-threaded environments.

Introduction to Blocked Queue​

Blocked Queue Operations​

Pseudocode​

Basic Operations​

Implementation in Python, C++, and Java​

Python Implementation​

C++ Implementation​

Java Implementation​

Complexity​

Example​

Conclusion​